Jamba-1.5: Hybrid Transformer-Mamba Models at Scale

We present Jamba-1.5, new instruction-tuned large language models based on our Jamba architecture. Jamba is a hybrid Transformer-Mamba mixture of experts architecture, providing high throughput and low memory usage across context lengths, while retaining the same or better quality as Transformer models. We release two model sizes: Jamba-1.5-Large, with 94B active parameters, and Jamba-1.5-Mini, with 12B active parameters. Both models are fine-tuned for a variety of conversational and instruction-following capabilties, and have an effective context length of 256K tokens, the largest amongst open-weight models. To support cost-effective inference, we introduce ExpertsInt8, a novel quantization technique that allows fitting Jamba-1.5-Large on a machine with 8 80GB GPUs when processing 256K-token contexts without loss of quality. When evaluated on a battery of academic and chatbot benchmarks, Jamba-1.5 models achieve excellent results while providing high throughput and outperforming other open-weight models on long-context benchmarks. The model weights for both sizes are publicly available under the Jamba Open Model License and we release ExpertsInt8 as open source.

Jamba: A Hybrid Transformer-Mamba Language Model

We present Jamba, a new base large language model based on a novel hybrid Transformer-Mamba mixture-of-experts (MoE) architecture. Specifically, Jamba interleaves blocks of Transformer and Mamba layers, enjoying the benefits of both model families. MoE is added in some of these layers to increase model capacity while keeping active parameter usage manageable. This flexible architecture allows resource- and objective-specific configurations. In the particular configuration we have implemented, we end up with a powerful model that fits in a single 80GB GPU. Built at large scale, Jamba provides high throughput and small memory footprint compared to vanilla Transformers, and at the same time state-of-the-art performance on standard language model benchmarks and long-context evaluations. Remarkably, the model presents strong results for up to 256K tokens context length. We study various architectural decisions, such as how to combine Transformer and Mamba layers, and how to mix experts, and show that some of them are crucial in large scale modeling. We also describe several interesting properties of these architectures which the training and evaluation of Jamba have revealed, and plan to release checkpoints from various ablation runs, to encourage further exploration of this novel architecture. We make the weights of our implementation of Jamba publicly available under a permissive license.

MRKL Systems: A modular, neuro-symbolic architecture that combines large language models, external knowledge sources and discrete reasoning

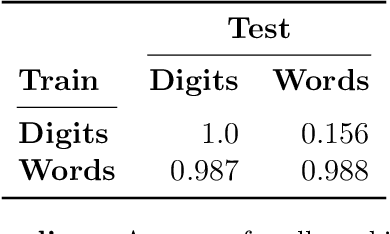
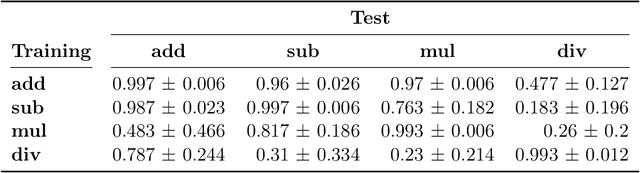
Huge language models (LMs) have ushered in a new era for AI, serving as a gateway to natural-language-based knowledge tasks. Although an essential element of modern AI, LMs are also inherently limited in a number of ways. We discuss these limitations and how they can be avoided by adopting a systems approach. Conceptualizing the challenge as one that involves knowledge and reasoning in addition to linguistic processing, we define a flexible architecture with multiple neural models, complemented by discrete knowledge and reasoning modules. We describe this neuro-symbolic architecture, dubbed the Modular Reasoning, Knowledge and Language (MRKL, pronounced "miracle") system, some of the technical challenges in implementing it, and Jurassic-X, AI21 Labs' MRKL system implementation.

Moser Flow: Divergence-based Generative Modeling on Manifolds

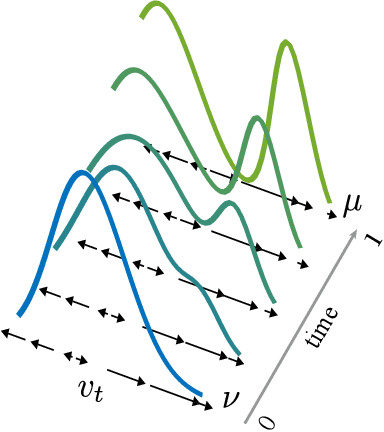
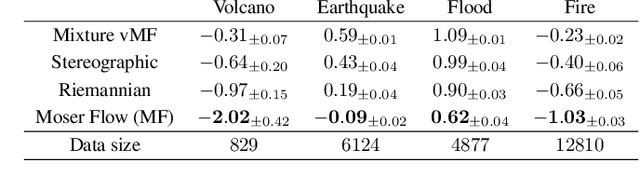
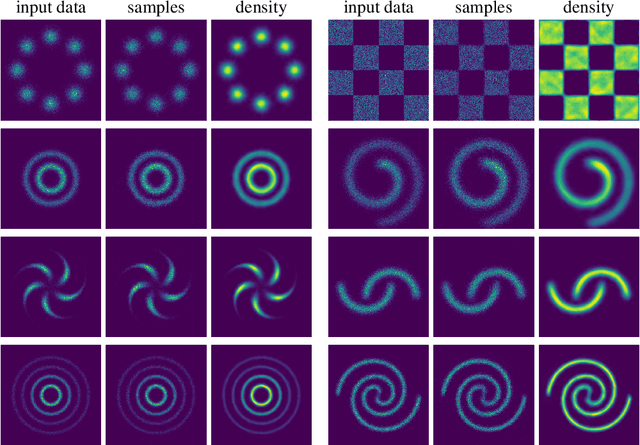
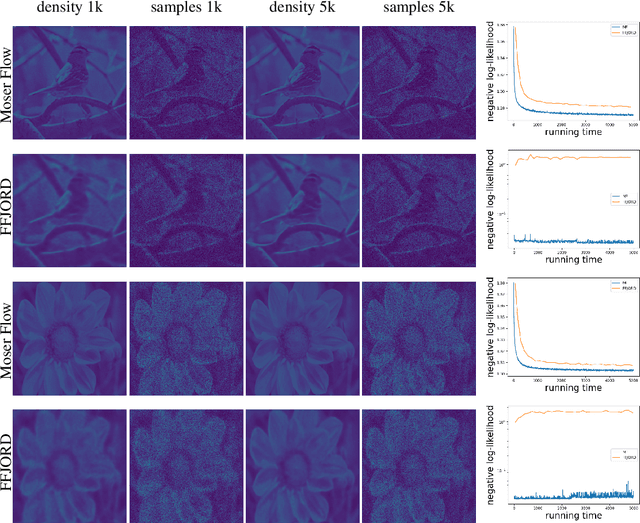
We are interested in learning generative models for complex geometries described via manifolds, such as spheres, tori, and other implicit surfaces. Current extensions of existing (Euclidean) generative models are restricted to specific geometries and typically suffer from high computational costs. We introduce Moser Flow (MF), a new class of generative models within the family of continuous normalizing flows (CNF). MF also produces a CNF via a solution to the change-of-variable formula, however differently from other CNF methods, its model (learned) density is parameterized as the source (prior) density minus the divergence of a neural network (NN). The divergence is a local, linear differential operator, easy to approximate and calculate on manifolds. Therefore, unlike other CNFs, MF does not require invoking or backpropagating through an ODE solver during training. Furthermore, representing the model density explicitly as the divergence of a NN rather than as a solution of an ODE facilitates learning high fidelity densities. Theoretically, we prove that MF constitutes a universal density approximator under suitable assumptions. Empirically, we demonstrate for the first time the use of flow models for sampling from general curved surfaces and achieve significant improvements in density estimation, sample quality, and training complexity over existing CNFs on challenging synthetic geometries and real-world benchmarks from the earth and climate sciences.